The New York Times Spelling Bee is a word puzzle where you try to make words using the letters provided.
You are given 7 letters with one denoted the ‘center’ letter. Your words can only use the provided letters – though letters can be used more than once – and must include the center letter. Words must be at least 4 letters long.
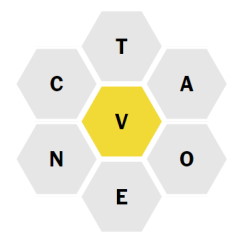
For example, for the above puzzle OCTAVE is a valid word. COVER is not since R is not a valid letter. Neither is OCTANE since it doesn’t use the letter V.
Frustratingly, the New York Times only lets you see which answers you missed on the next day after the puzzle is released! This motivated me to write my own solver, and in the process find an interesting way to test words against the puzzle’s rules.
We’ll walk through the steps to write a C++ program which, given a puzzle as input, outputs all the valid words you can make.
1 – Reading the puzzle
We’ll start by providing a way to input the source letters to the program. We’ll do this as a single line of input, using upper case letters. We’ll assume a convention where the first letter in the input is the center letter.
For example, for the above puzzle, the input would be ‘VCTAOEN’.
int main()
{
// read the source letters
std::cout << "Enter letters: ";
std::string source_letters;
std::cin >> source_letters;
return 0;
}2 – Generating words
The first step to solving a word puzzle like this is realizing there’s no way to generate words from the English language. Instead we’ll need to find an existing dictionary of words we can use, and check if each one is a valid solution. You’ll find there are many word lists freely available online.
I’ll use this one, and save it as dictionary.txt.
Note that no word list is perfect, since there’s simply no authoritative definition of what an English word is. And in the case of the Spelling Bee, official answers are chosen by an editor.
Once we have a suitable word list, we need to load the words for use in our program. We’ll filter out any words shorter than 4 letters at this point.
std::vector<std::string> dictionary_words;
std::cout << "Loading dictionary..." << std::endl;
std::ifstream dictionary("dictionary.txt");
std::string line;
while (std::getline(dictionary, line))
{
const int MIN_WORD_LENGTH = 4;
if (line.length() >= MIN_WORD_LENGTH)
{
dictionary_words.push_back(line);
}
}3 – Checking if a word is valid
We have our source letters and a list of dictionary words, now we need a way to check if a given dictionary word is a valid solution. Let’s write a function for this.
We need to check two things: that each letter in our word is one of the source letters, and that the center letter (the first source letter) is contained in our word.
bool is_valid_word(const std::string& word, const std::string& source_letters)
{
// check if each letter in the test word is one of the source letters
for (int word_idx = 0; word_idx < word.length(); word_idx++)
{
bool is_source_letter = false;
for (int source_idx = 0; source_idx < source_letters.length(); source_idx++)
{
if (word[word_idx] == source_letters[source_idx])
{
is_source_letter = true;
break;
}
}
if (!is_source_letter)
{
return false;
}
}
// check that the center letter is contained in our test word
for (int word_idx = 0; word_idx < word.length(); word_idx++)
{
if (word[word_idx] == source_letters[0])
{
return true;
}
}
return false;
}4 – Generating solutions
Now all that’s left is to call this function for every word in our dictionary and output the valid results.
std::vector<std::string> solutions;
for (int idx = 0; idx < dictionary_words.size(); idx++)
{
if (is_valid_word(dictionary_words[idx], source_letters))
{
solutions.push_back(dictionary_words[idx]);
}
}
std::cout << solutions.size() << " solution(s)" << std::endl;
for (int idx = 0; idx < solutions.size(); idx++)
{
std::cout << solutions[idx] << std::endl;
}5 – Testing the solver
Let’s try the solver on the puzzle above.
Enter letters: VCTAOEN
Loading dictionary…
24 solution(s)
CAVE
CAVEAT
CONCAVE
CONVECT
CONVENE
CONVENT
COVE
COVEN
COVENANT
COVET
EVEN
EVENT
NAVE
NONEVENT
OCTAVE
OCTAVO
OVATE
OVEN
VACANT
VACATE
VANE
VENT
VETO
VOTE
Not bad! We can compare against the official answer list on this unofficial archive.
We did miss a few words (AVOCET, CAVA, EAVE, NOVA, NOVAE) and include one word that wasn’t in the official answer list (OCTAVO).
6 – More efficient word checking
It’s my job as a game programmer to write code which doesn’t just do the job, but does it in a performant way. ‘Hot code’ – ie. the code which runs most frequently in the program – is usually the best place to start when optimizing. In our case that’s the is_valid_word function we wrote.
Let’s start with a couple observations about the way we’re checking validity:
1. We’re checking every letter of the test word against the source letters, even though some letters may be duplicated.
2. We are iterating over all the source letters to check for each letter in the word. And we’re iterating over all the letters in the word to check for the center letter.
To improve on both these points, we’re going to change the way we represent words. Rather than an ordered series of characters, we can think of words as just the set of letters they contain. And rather than actually storing each of these letters, we just need to store a true or false value for each of the 26 letters in the alphabet.
CAVEAT = { A = true, B = false, C = true, D = false, E = true... }
This naturally lends itself to a binary representation, where each bit is 1 or 0 indicating if the letter at that position in the alphabet is present in the word.
CAVEAT = 10101000000000000001010000
This new representation uses 26 bits of information to store a word. We’ve essentially compressed our data, stripping out any redundant information (letter counts, letter positions) which are not needed for this puzzle.
Once we put our test word, source letters, and center letter into this ‘packed’ representation, we can see how much simpler the problem of checking validity becomes.
To check if the test word contains the center letter, we now just need to check that the test word contains a 1 at the same bit as the center letter, which can be achieved with a bitwise AND between the two binary representations.

And to check if all the letters in the test word are included in the source letters, we want to check that all the bits with a 1 in the test word also have a 1 in the source letters. This can be achieved by performing a bitwise AND between the two binary representations, and then checking that the result is equivalent to the test word. (Note how this corresponds to a necessary and sufficient property of a subset relationship in set theory.)

Now to implement this in our program. First we’ll write functions for creating this ‘packed’ representation from a word or letter.
int32_t pack_letter(char letter)
{
return 1 << (letter - 'A');
}
int32_t pack_word(const std::string& word)
{
int32_t packed = 0;
for (int idx = 0; idx < word.length(); idx++)
{
packed |= pack_letter(word[idx]);
}
return packed;
}Next we can write our validity check.
bool is_valid_word(int32_t word, int32_t source_letters, int32_t center_letter)
{
return (word & center_letter) && ((word & source_letters) == word);
}And finally use this to generate solutions.
std::vector<int32_t> packed_dictionary_words;
packed_dictionary_words.resize(dictionary_words.size());
for (int idx = 0; idx < dictionary_words.size(); idx++)
{
packed_dictionary_words[idx] = pack_word(dictionary_words[idx]);
}
const int32_t packed_source_letters = pack_word(source_letters);
const int32_t packed_center_letter = pack_letter(source_letters[0]);
for (int idx = 0; idx < dictionary_words.size(); idx++)
{
if (is_valid_word(packed_dictionary_words[idx], packed_source_letters, packed_center_letter))
{
solutions.push_back(dictionary_words[idx]);
}
}To evaluate performance I ran each version of the solver 10 times for 10 different puzzle inputs and noted the average time.
| Original | 406 µs |
| Packed (excluding dictionary packing) | 95 µs |
| Packed (including dictionary packing) | 651 µs |
Using the ‘packed’ approach, we’ve achieved a 4x speedup for word checking. This excludes the cost of initially packing the words in the dictionary, but if we include the packing cost our new solution is actually slower! That means for a program intended to only run once this new approach is a poor choice. But because packing the dictionary is a pre-computation step, independent of our puzzle input, we could trivially store the packed representation of each word as part of our dictionary. This more efficient checking would also provide an advantage if we were solving a different puzzle that required testing each word multiple times.
7 – Conclusion
The Spelling Bee is a good introduction to programmatic word puzzle-solving and provides a look at how word puzzles relate to set theory and efficient ways to represent this data.
Full source code for the solver is available here.
